Sea of WAVES

Waves

Waves appear in many forms and shapes. They have their own properties and behave differently from each other

Wave is a disturbance or variation which travels through a medium. They are characterized by wavelength, frequency, and the speed at which they move.

Standing waves don’t form under just any circumstances. They require that energy be fed into a system at an appropriate frequency

Image result for parts of a wave

Parts of waves

  • Amplitude- the maximum positive displacement from the undisturbed position of the medium to the top of a crest.
  • Crest– section of the wave that rises above the undisturbed position.
  • Through– a section which lies below the undisturbed position.
  • Wavelength- wavelength of a wave is the distance between any two adjacent corresponding locations on the wave train.

Nodes and Antinodes

Cartoon representation of a standing wave with nodes and antinodes identified

Node is a point along a standing wave where the wave has minimum amplitude.

Example:

  • In a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the note played.

Antinodes are where the amplitude (positive of negative) is a maximum, halfway between two adjacent nodes.

 

Harmonic Motion

Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke’s Law.

The motion is sinusoidal in time and demonstrates a single resonant frequency.

 

 

 

 

Simple Harmonic Motion, maximum speed occurs at x = 0 (the equilibrium level or position), and speed is zero at the extreme ends ( x = +/- A ). Acceleration has a different story. At the middle (x = 0), acceleration is zero

The simple harmonic solution is


with  being the natural frequency of the motion.

The period of a simple pendulum is

T=2\pi \sqrt{\frac{L}{g}},

where L is the length of the string and g is the acceleration due to gravity

 

 

Types of Harmonic Motion

  1. Mass Spring Oscillator

The simplest example of an oscillating system is a mass connected to a rigid foundation by way of a spring.

The spring constant k provides the elastic restoring force, and the inertia of the mass m provides the overshoot. By applying Newton’s second law F=ma to the mass, one can obtain the equation of motion for the system where  is the natural oscillating frequency. The solutions to this equation of motion takes the form


where xm is the amplitude of the oscillation, and φ is the phase constant of the oscillation. Both xm and φ are constants determined by the initial condition (intial displacement and velocity) at time t=0 when one begins observing the oscillatory motion.

For a spring-mass system, such as a block attached to a spring, the spring force is responsible for the oscillation.
F_s = -kxFs​=−kxF, start subscript, s, end subscript, equals, minus, k, x

Note: Calculate the time of one oscillation or the period (T) by dividing the total time by the number of oscillations you counted. Use your calculated (T) along with the exact length of the pendulum (L) in the above formula to find “g.”

  1. Simple Pendulum

A simple pendulum has a small-diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably.

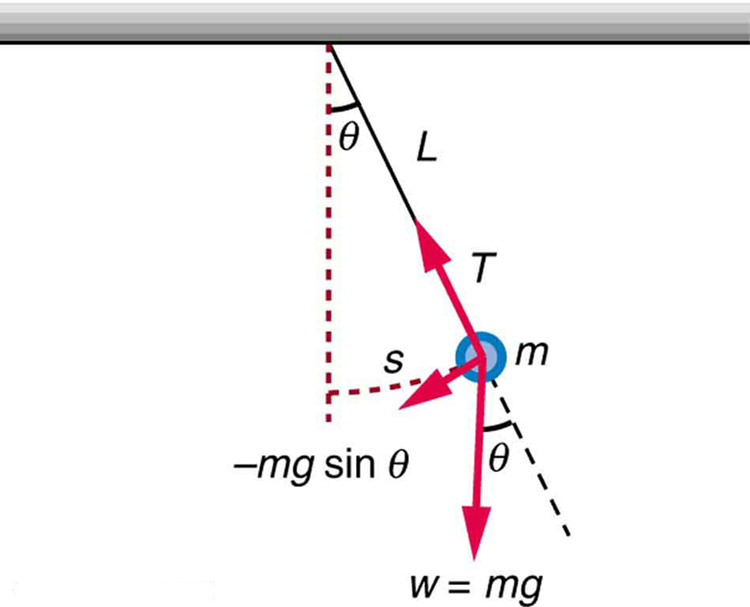
In the figure, a horizontal bar is drawn. A perpendicular dotted line from the middle of the bar, depicting the equilibrium of pendulum, is drawn downward. A string of length L is tied to the bar at the equilibrium point. A circular bob of mass m is tied to the end of the string which is at a distance s from the equilibrium. The string is at an angle of theta with the equilibrium at the bar. A red arrow showing the time T of the oscillation of the mob is shown along the string line toward the bar. An arrow from the bob toward the equilibrium shows its restoring force asm g sine theta. A perpendicular arrow from the bob toward the ground depicts its mass as W equals to mg, and this arrow is at an angle theta with downward direction of string.

Simple pendulum consists of a mass m hanging from a string of length L and fixed at a pivot point P. When displaced to an initial angle and released, the pendulum will swing back and forth with periodic motion. By applying Newton’s second law for rotational systems, the equation of motion for the pendulum may be obtained

,and rearranged as

.
If the amplitude of angular displacement is small enough that the small angle approximation () holds true, then the equation of motion reduces to the equation of simple harmonic motion 

.